Solved Assume That N Is A Positive Integer Use Mathematical I In this section, we will learn a new proof technique, called mathematical induction, that is often used to prove statements of the form \((\forall n \in \mathbb{n})(p(n))\). in section 4.2 , we will learn how to extend this method to statements of the form \((\forall n \in t) (p(n))\), where \(t\) is a certain type of subset of the integers. Lecture 2: mathematical induction mathematical induction is a technique used to prove that a certain property holds for every positive integer (from one point on). principle of mathematical induction. for each (positive) integer n, let p(n) be a statement that depends on n such that the following conditions hold: (1) p(n.
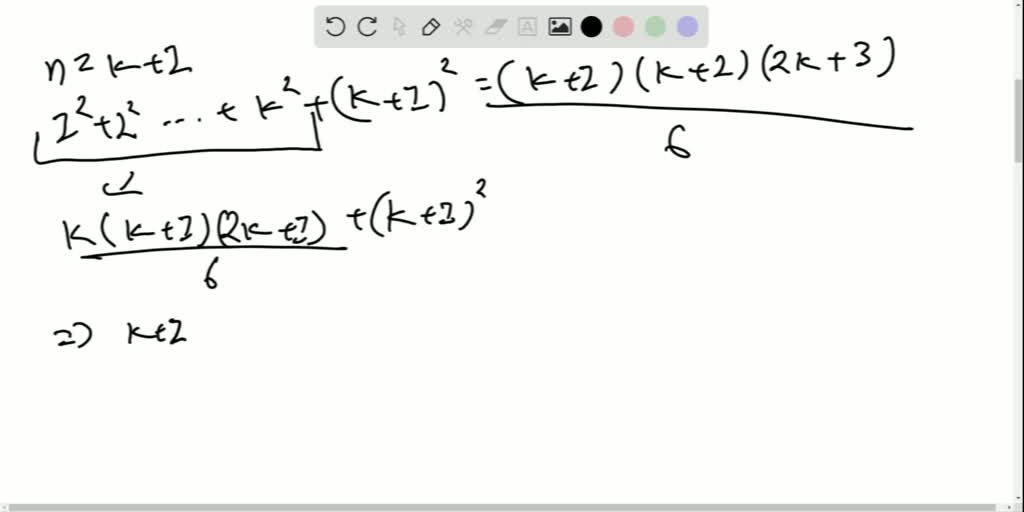
Solved Use Mathematical Induction To Prove Each Statement Ass Exercise 3.4.10. use mathematical induction to show that n ∑ i = 1 i 4 i(i 1)(i 2) = n(3n 7) 2(n 1)(n 2) for all integers n ≥ 1. this page titled 3.4: mathematical induction an introduction is shared under a license and was authored, remixed, and or curated by () . mathematical induction can be used to prove that an identity. Example: use mathematical induction to prove that n3 − n is divisible by 3, for every positive integer n. solution: let p(n) be the proposition that 3 | (n3 − n). –basis: p(1) is true since 13 − 1 = 0, which is divisible by 3. –induction: assume p(k) holds, i.e., k3 − k is divisible by 3, for an arbitrary positive integer k. Prove the inductive step, p (k) → p (k 1), by assuming that p (k) is true, called the inductive hypothesis, then prove that p (k 1) is also true. use the principle of mathematical induction to prove that p (n) is true for all integers n ≥ a. in many examples a = 1 or a = 0, but it is possible to start induction using any integer base a. Mathmatical induction. mathmatical induction can be used to prove statements that assert that p(n) is true for all positive integers n where p(n) is a propositional function. propositional function – in logic, is a sentence expressed in a way that would assume the value of true or false, except that within the sentence is a variable (x) that.
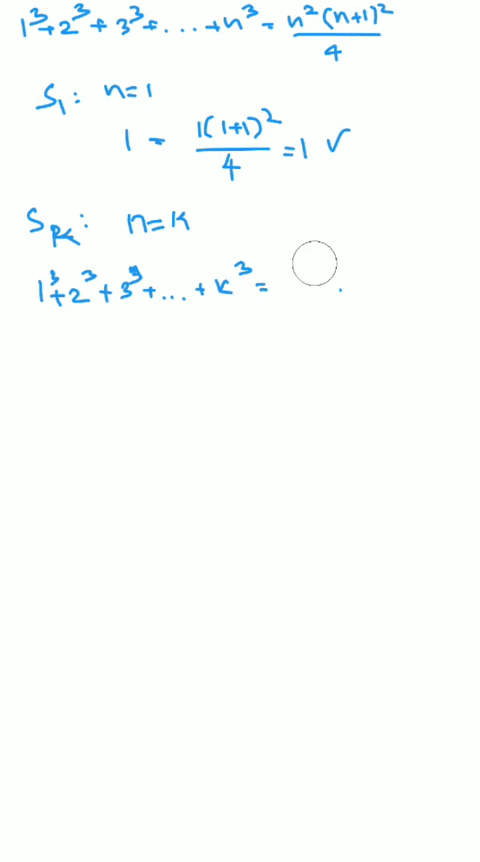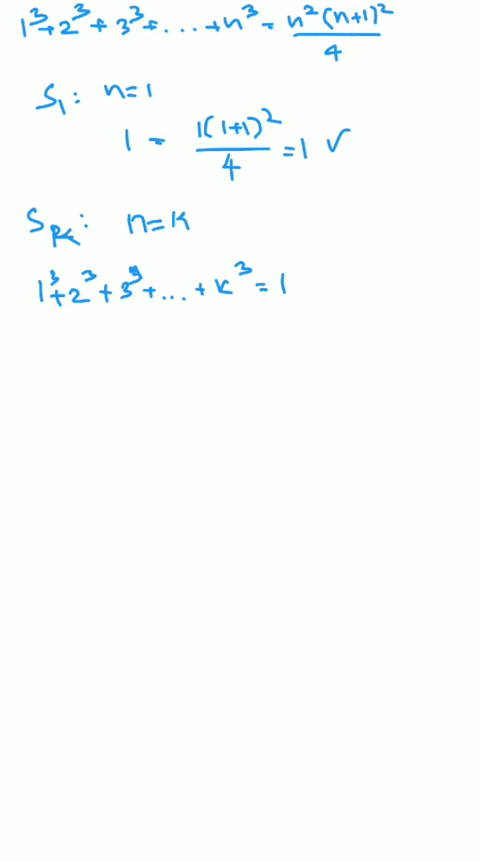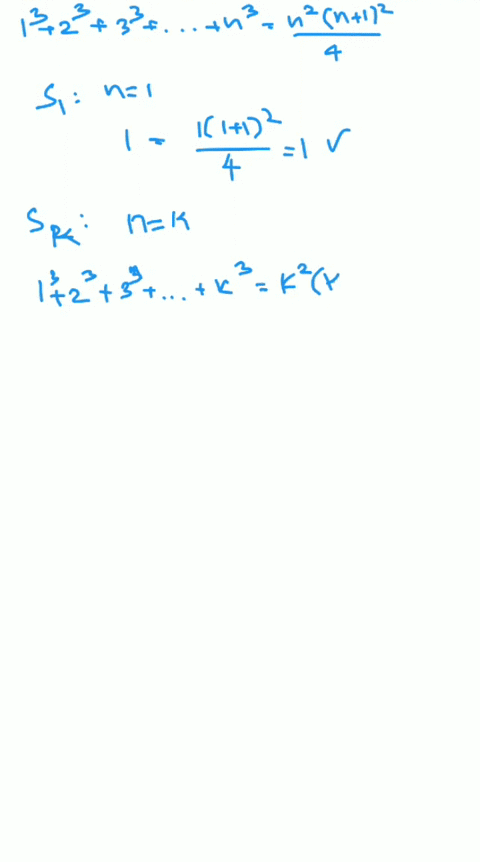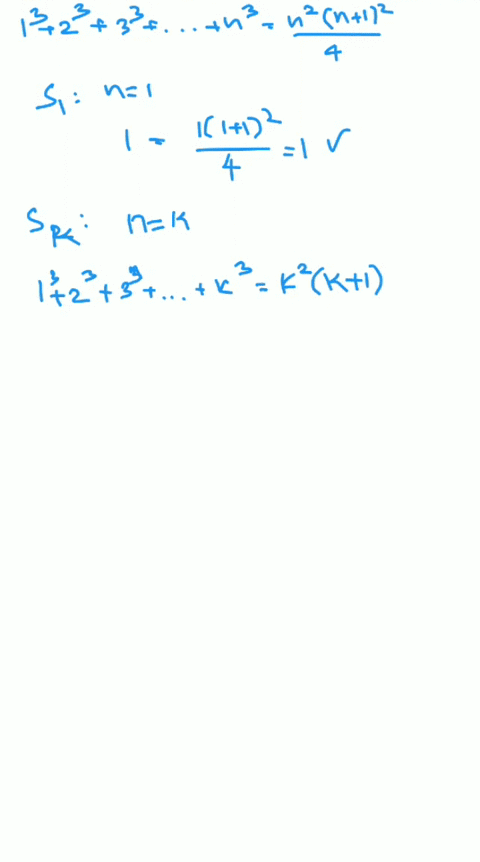
Solved Use Mathematical Induction To Prove Each Statement Ass Prove the inductive step, p (k) → p (k 1), by assuming that p (k) is true, called the inductive hypothesis, then prove that p (k 1) is also true. use the principle of mathematical induction to prove that p (n) is true for all integers n ≥ a. in many examples a = 1 or a = 0, but it is possible to start induction using any integer base a. Mathmatical induction. mathmatical induction can be used to prove statements that assert that p(n) is true for all positive integers n where p(n) is a propositional function. propositional function – in logic, is a sentence expressed in a way that would assume the value of true or false, except that within the sentence is a variable (x) that. Solved examples. using mathematical induction, prove the given statement: for any natural number n, 22n – 1 is divisible by 3. solution: considering n = 1, we get, 2 2 (1) – 1 = 2 2 – 1 = 4 – 1 = 3, divisible by 3. thus, the given statement is true for n = 1. assuming n = k, the statement 2 2k – 1 is divisible by 3. Hence, by the principle of mathematical induction, p(n) is true for all natural numbers n. important notes on principle of mathematical induction. each mathematical statement is assumed as p(n) for a natural number n. first, we prove for n = 1, then assume for n = k and finally prove for n = k 1.
Comments are closed.