Singular Value Decomposition Svd Dominant Correlations

Schematic Representation For Singular Value Decomposition Svd This lectures discusses how the svd captures dominant correlations in a matrix of data. these lectures follow chapter 1 from: "data driven science and engi. Singular value decomposition. i can multiply columns uiσi from uΣ by rows of vt: svd a = uΣv t = u 1σ1vt ··· urσrvt r. (4) equation (2) was a “reduced svd” with bases for the row space and column space. equation (3) is the full svd with nullspaces included. they both split up a into the same r matrices u iσivt of rank one: column.

Singular Value Decomposition Svd Dominant Correlations Resourcium A singular value decomposition (svd) is a generalization of this where ais an m nmatrix which does not have to be symmetric or even square. 1 singular values let abe an m nmatrix. before explaining what a singular value decom position is, we rst need to de ne the singular values of a. consider the matrix ata. this is a symmetric n nmatrix, so its. Singular value decomposition (svd) in linear algebra, the singular value decomposition (svd) is a factorization of a real or complex matrix that generalizes the eigendecomposition of a square normal matrix to any m × n matrix via an extension of the polar decomposition. from singular value decomposition see more. this is all we have. Singular value decomposition. the singular value decomposition of a matrix is usually referred to as the svd. this is the final and best factorization of a matrix: a = uΣvt. where u is orthogonal, is diagonal, and v is orthogonal. Σ. in the decomoposition a = u vt , a can be any matrix. we know that if a. 2 the singular value decomposition here is the main intuition captured by the singular value decomposition (svd) of a matrix: an m nmatrix aof rank rmaps the r dimensional unit hypersphere in rowspace(a) into an r dimensional hyperellipse in range(a). 2at least geometrically. one solution may be more e cient than the other in other ways. 3.
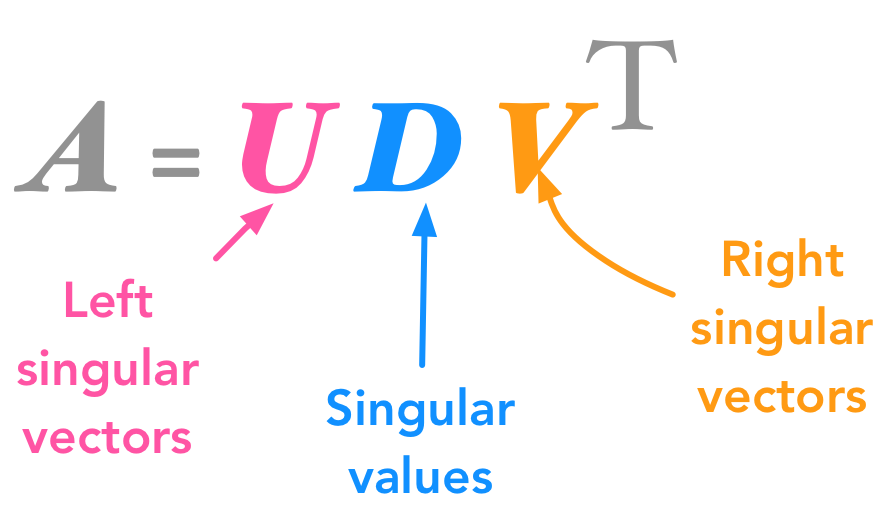
Introduction To Singular Value Decomposition Using Python Numpy Singular value decomposition. the singular value decomposition of a matrix is usually referred to as the svd. this is the final and best factorization of a matrix: a = uΣvt. where u is orthogonal, is diagonal, and v is orthogonal. Σ. in the decomoposition a = u vt , a can be any matrix. we know that if a. 2 the singular value decomposition here is the main intuition captured by the singular value decomposition (svd) of a matrix: an m nmatrix aof rank rmaps the r dimensional unit hypersphere in rowspace(a) into an r dimensional hyperellipse in range(a). 2at least geometrically. one solution may be more e cient than the other in other ways. 3. We can also rewrite the decomposition using the properties of matrix multiplication. x = δ1[∣ u1 ∣][− vt1 −] … δr[∣ ur ∣][− vtr −] x = r ∑ k = 1δkukvtk. because both u and v are orthonormal all their r vectors are having unit length and they are thus reshaped by the singular values. Linear independence. c1v 1 c2v 2 c3v 3 · · · cnv n = 0 ⇔ c1 = c2 = · · · = cn = 0. if n vectors are not linearly independent, then they span a subspace of dimension < n. eg. two vectorsv 1 andv 2 are linearly dependent if and only if they are multiples of each other:v 1 = av 2. in this casev 1 v 2 only span a 1 dimensional.

How To Use Singular Value Decomposition Svd In Machine Learning We can also rewrite the decomposition using the properties of matrix multiplication. x = δ1[∣ u1 ∣][− vt1 −] … δr[∣ ur ∣][− vtr −] x = r ∑ k = 1δkukvtk. because both u and v are orthonormal all their r vectors are having unit length and they are thus reshaped by the singular values. Linear independence. c1v 1 c2v 2 c3v 3 · · · cnv n = 0 ⇔ c1 = c2 = · · · = cn = 0. if n vectors are not linearly independent, then they span a subspace of dimension < n. eg. two vectorsv 1 andv 2 are linearly dependent if and only if they are multiples of each other:v 1 = av 2. in this casev 1 v 2 only span a 1 dimensional.

Comments are closed.