Question Video Finding The Measure Of Consecutive Interior Angles

Question Video Finding The Measure Of Consecutive Interior Angles Given that the interior angles in a quadrilateral sum to 360 degrees, we can write that the four angles of 62 degrees plus 56 degrees plus 124 degrees plus the measure of angle 𝐷 equals 360 degrees. simplifying the left hand side, we have that 242 degrees plus the measure of angle 𝐷 equals 360 degrees. Example 1: same side interior angles. calculate the size of the missing angle x. x. justify your answer. highlight the angle (s) that you already know. the given angle is 113∘. 113∘. 2 use same side interior angles to find a missing angle. here, you can label the co interior angle on the diagram as 60∘ 60∘ as 113 67=180. 113 67 = 180.

Question Video Finding The Measure Of An Angle Using Consecutive Example 2: use the consecutive interior angles theorem to find the value of angle 'x' if line 1 and line 2 are parallel. solution: in the figure, it is given that 40° and ∠x are consecutive interior angles and 'line 1' and 'line 2' are parallel. by the consecutive interior angles theorem, ∠x and 40° are supplementary. First, we need to consider the definition of consecutive interior angles. they are the pair of angles on one side of the transversal but inside the two lines. if we have two lines and a transversal, here are two consecutive angles. they fall on the same side of the transversal and inside the two lines. so, let’s consider our five options. Let us take some example to understand the concept better, find the value of x, y and z in the given figure. solution: according to the theorem of consecutive interior angles if the two lines intersected by the transversal are parallel, the consecutive interior angles are supplementary. thus, ∠50° x = 180°. When two lines are crossed by another line (called the transversal): the pairs of angles on one side of the transversal but inside the two lines are called consecutive interior angles. in this example d and f are consecutive interior angles. also c and e are consecutive interior angles. to help you remember: the angle pairs are consecutive.

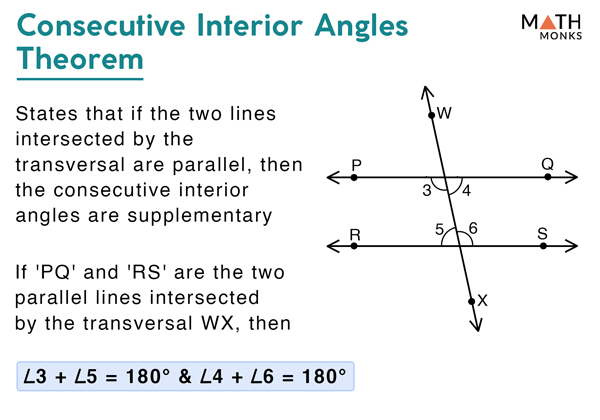
Consecutive Interior Angles вђ Definition Theorem With Examples Let us take some example to understand the concept better, find the value of x, y and z in the given figure. solution: according to the theorem of consecutive interior angles if the two lines intersected by the transversal are parallel, the consecutive interior angles are supplementary. thus, ∠50° x = 180°. When two lines are crossed by another line (called the transversal): the pairs of angles on one side of the transversal but inside the two lines are called consecutive interior angles. in this example d and f are consecutive interior angles. also c and e are consecutive interior angles. to help you remember: the angle pairs are consecutive. The consecutive interior angle theorem states that any pair of consecutive interior angles are supplementary (or add up to 180°). this means that given the consecutive interior angles, ∠3 & ∠5 and ∠4 & ∠6, each pair will add up to 180°. ∠3 ∠5 = 180°. ∠4 ∠6 = 180°. keep this property in mind when solving problems. Identify the pairs of consecutive interior and exterior angles in the given figure. solution: pairs of consecutive interior angles: ∠3 and ∠5; ∠4 and ∠6. pairs of consecutive exterior angles: ∠1 and ∠7; ∠2 and ∠8. a pair of consecutive interior angles formed by lines p and q are 106 and 73.