Laplace Transform Derivatives Theorem Proofs First Second Third

Laplace Transform Derivatives Theorem Proofs First Second Third For first order derivative: $\mathcal{l} for second order derivative: proof of laplace transform of derivatives. The laplace transform †deflnition&examples †properties&formulas { linearity { theinverselaplacetransform { timescaling { exponentialscaling { timedelay { derivative { integral { multiplicationbyt { convolution 3{1.

Laplace Transform Derivatives Theorem Proofs First Second Third Let us see how the laplace transform is used for differential equations. first let us try to find the laplace transform of a function that is a derivative. suppose g(t) is a differentiable function of exponential order, that is, | g(t) | ≤ mect for some m and c. so l{g(t)} exists, and what is more, limt → ∞e − stg(t) = 0 when s> c. This is a simple algebraic equation that we can easily solve for y(s). first, gather the y(s) terms together and add 4 to both sides, [s −3]y(s) = 4 , and then divide through by s −3, y(s) =. 4 s −3. thus, we have the laplace transform y of the solution y to the original initial value problem. Multiplying both sides of (24) = −2 ± 皼是by the left hand side denominator, equate coefficients and solve for residues as before: 楄ু楄ু 1. laplace transform of the. step response is Ɲ曪= 0. 0625 Ɲ曫− 2 2 2 (25) the time domain step response of the system is the. two decaying sinusoids: yy tt = 0. 0625 − 0. 0625ee. The one sided laplace transform is defined as. (1) l {f (t)} = f (s) = ∫ 0 − ∞ e − s t f (t) d t. in this equation. l symbolizes the laplace transform. f (s) is the laplace domain equivalent of the time domain function f (t). the lower limit of 0 − emphasizes that the value at t = 0 is entirely captured by the transform.

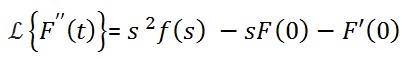
Laplace Transform Derivatives Theorem Proofs First Second Third Multiplying both sides of (24) = −2 ± 皼是by the left hand side denominator, equate coefficients and solve for residues as before: 楄ু楄ু 1. laplace transform of the. step response is Ɲ曪= 0. 0625 Ɲ曫− 2 2 2 (25) the time domain step response of the system is the. two decaying sinusoids: yy tt = 0. 0625 − 0. 0625ee. The one sided laplace transform is defined as. (1) l {f (t)} = f (s) = ∫ 0 − ∞ e − s t f (t) d t. in this equation. l symbolizes the laplace transform. f (s) is the laplace domain equivalent of the time domain function f (t). the lower limit of 0 − emphasizes that the value at t = 0 is entirely captured by the transform. Theorem. let f: r → r or r → c be a continuous function, differentiable on any interval of the form 0 ≤ t ≤ a. let f be of exponential order a. let l{f} denote the laplace transform of f. let f be piecewise continuous with one sided limits on said intervals. then l{f} exists for re(s)> a, and:. Laplace transform i 5 the rst limit is zero by the bound on f since je stf(t)j ke (s a)t!0 as t !1: for the second limit, we can take b !1since we have already established the improper integral converges in the proof that l[f] exists. this result can be iterated to nd the laplace transform of higher order derivatives. for example,.

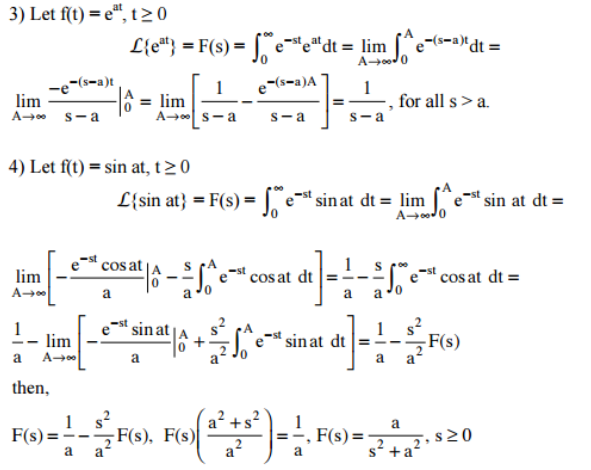
Laplace Transform Definition Formula Properties And Examples Theorem. let f: r → r or r → c be a continuous function, differentiable on any interval of the form 0 ≤ t ≤ a. let f be of exponential order a. let l{f} denote the laplace transform of f. let f be piecewise continuous with one sided limits on said intervals. then l{f} exists for re(s)> a, and:. Laplace transform i 5 the rst limit is zero by the bound on f since je stf(t)j ke (s a)t!0 as t !1: for the second limit, we can take b !1since we have already established the improper integral converges in the proof that l[f] exists. this result can be iterated to nd the laplace transform of higher order derivatives. for example,.